Quick intro: Introduction to Numpy

Introduction to Numpy

Source Code: Google Drive Link

NumPy (Numerical Python) is one of the core packages for numerical computing in Python. Pandas, Matplotlib, Statmodels and many other Scientific libraries rely on NumPy.

In simple regular python, it takes up a lot of space to simply store a number. Because, python is a high level object oriented programming language. But, if we mean business, then we need it to work fast and efficiently.

import numpy as np

np.int8 #defining the space number can use. int8 means it can use 8 bits. 

 

Again numpy is an array processing library.

If you have list of numbers in python. the list might show a lot of incongruity in  storing the data into the memory. 

But if you use the array system of numpy that is not going to happen.

 

 

 

import sys
import numpy as np

np.array([1, 2, 3, 4])

#lets create two arrays

a = np.array([1, 2, 3, 4])

b = np.array([0, .5, 1, 1.5, 2])

#accessing elements of the array

a[1],b[3] #arryaname[position-in-third-bracket]

a[0:]

b[0:3]

a[1:-1]

a[-1]

a[1:-2] #this will print only 2.

b #multi indexing

b[0], b[2], b[-1]

b[[0, 2, -1]] #result will be another numpy array

k=b[[0, 2, -1]] #if you save the array in k. this happens.

#copy and paste these into jupyter lab to see the execution.

b.dtype #how to check the data type in an array 

y = np.array([1, 2, 3, 4], dtype=np.float) #how to assign dtype to an array

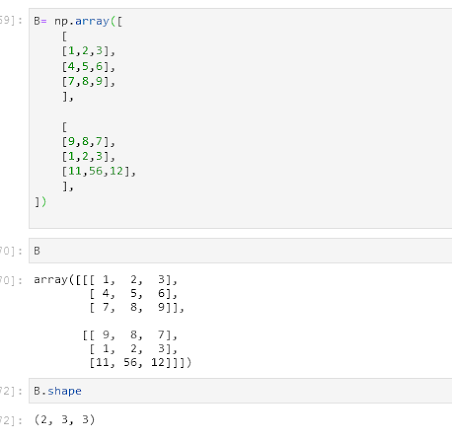
#Writing a three dimensional array:
B= np.array([
    [
    [1,2,3],
    [4,5,6],
    ],
    [
    [9,8,7],
    [1,2,3],
    ],
])

#indexing and slicing matrices

# Square matrix
A = np.array([
#.   0. 1. 2
    [1, 2, 3], # 0
    [4, 5, 6], # 1
    [7, 8, 9]  # 2
])

A[1:, :2]
#this is what the code will give you 

#output: 

array([[4, 5],
       [7, 8]])

#modifying an array: 

A[1]=np.array([10,10,10])

#output:

array([[ 1,  2,  3],
       [10, 10, 10],
       [ 7,  8,  9]])

#expanding the input to all cells (columns) of a row 

A[1]=99

#output:

A

array([[ 1,  2,  3],
       [99, 99, 99],
       [ 7,  8,  9]])

Statistical Methods of numpy:

A = np.array([
#.   0. 1. 2
    [1, 2, 3], # 0
    [4, 5, 6], # 1
    [7, 8, 9]  # 2
])

A.sum()

A.mean()

A.std()

Axis Issues: What is axis?

A = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]

    #12,15,18  #this is the A.sum(axis=0) output (Vertical)
])

A.sum(axis=0)

#output: array([12, 15, 18])

 

#If its axis = 1

A.sum(axis=1)

@output=

array([ 6, 15, 24])(horizontal)

 

 

Shape of a numpy array:

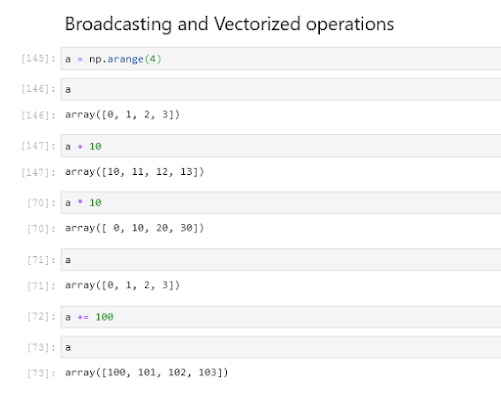
Numpy Array: Broadcasting and Vectorized Operations

#Try these codes below:

a = np.arange(4) #gives you array([0, 1, 2, 3])

b = np.array([10, 10, 10, 10])

a + b (#adds along the axis 0)

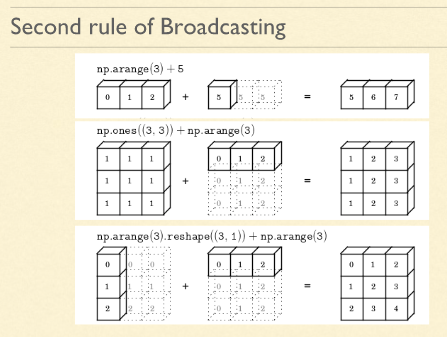
See the chart and you will learn it all

 

Boolean Arrays and Operations :
Lets say we have an array 1D

n= np.array([1,2,3]) 

#We want to find if  any of the elements is divisible by two and with no reminder:
g = (n%2 == 0) #find the values that is divisible by two with no reminder. 

g

Lets say we have an array 2D

import numpy as np

a = np.reshape(np.arange(16), (4,4))

#This will give you this array: 

[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]
 [12 13 14 15]]

#type in the following code
large_values = (a > 10) # test which elements of a are greater than 10
print(large_values)


Type in Code:
c = (a%2 == 0) | (a%3 == 0) 

# test which elements of a are divisible by either 2 or 3

print('array a:\n{}\n'.format(a))
print('array c:\n{}'.format(c))

#output:

array a: [[ 0 1 2 3] [ 4 5 6 7] [ 8 9 10 11] [12 13 14 15]]

array c: [[ True False True True] [ True False True False] [ True True True False] [ True False True True]]

If you want to get an item that is bigger than the average:
code:
a[a > a.mean()] #this command will give you a list of items.
a>a.mean() #this command will give you true false binary output.

Linear Algebra:

Lets say following we have two arrays:

A = np.array([
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]
])

B = np.array([
    [6, 5],
    [4, 3],
    [2, 1]
])

A @ B # A.dot(B)

Output:
array([[20, 14],
       [56, 41],
       [92, 68]])

Nowlets try :

B.T